PAA Sum of Subsets Backtraking
Description
O problema “Sum of Subsets” é um desafio emblemático na área de ciência da computação, situando-se na categoria dos problemas de decisão. O enigma consiste em determinar a existência de um subconjunto de números, dentro de um conjunto fornecido de inteiros, que totalize um valor alvo definido. Este é uma forma específica do problema de “Subconjunto de Soma” (Subset Sum Problem), que por sua vez, é um caso particular do problema da mochila (Knapsack Problem).
A essência do problema “Sum of Subsets” reside na sua classificação como NP-completo, indicando que, até o momento, não existe algoritmo de tempo polinomial conhecido que o resolva de maneira eficiente em todos os cenários. Estratégias comuns para sua solução incluem a utilização de técnicas de backtracking, que exploram as possibilidades de forma sistemática, retrocedendo assim que determina-se a inviabilidade de um conjunto candidato a solução, o que potencialmente reduz o espaço de busca em comparação com uma abordagem de força bruta.
Este problema é relevante em diversas aplicações práticas, tais como na área de otimização, onde é necessário selecionar um subconjunto ótimo de elementos para alcançar um objetivo específico, e na criptografia, onde a dificuldade de resolução contribui para a segurança. Trabalhar com o problema “Sum of Subsets” desenvolve competências importantes em lógica computacional e técnicas de backtracking.
brute force
Geramos todas as combinações possíveis em um vetor de bits, onde cada bit representa se o elemento correspondente deve estar no subconjunto ou não.
Exemplo:
# The array [5, 4, 9] has the following subsets:
#[5 4 9] = [5, 4, 9]
# 0 0 1 -> 9 = 9
# 0 1 0 -> 4 = 4
# 0 1 1 -> 4 + 9 = 13
# 1 0 0 -> 5 = 5
# 1 0 1 -> 5 + 9 = 14 CORRETO
# 1 1 0 -> 5 + 4 = 9
# 1 1 1 -> 5 + 4 + 9 = 18Table:
| Subset | Binary | Sum | Target Sum | Result |
|---|---|---|---|---|
| [5] | 001 | 5 | 14 | False |
| [4] | 010 | 4 | 14 | False |
| [4, 5] | 011 | 9 | 14 | False |
| [9] | 100 | 9 | 14 | False |
| [5, 9] | 101 | 14 | 14 | True |
| [4, 5] | 110 | 9 | 14 | False |
| [4, 5, 9] | 111 | 18 | 14 | False |
code
def subset_sum_bruteforce(array: List[int], target_sum: int) -> Tuple[List[int], int] | None:
n = len(array)
expanded = 0
# Gera todas combinações possíveis
for i in range(1, 2 ** n):
subset = []
subset_sum = 0
expanded += 1
# Para cada bit, verifica se o elemento correspondente deve estar no subconjunto
for j in range(n):
# Se o bit j estiver ligado, o elemento j é adicionado ao subconjunto
if (i >> j) & 1:
subset.append(array[j])
subset_sum += array[j]
# Se a soma do subconjunto for igual ao objetivo, retorna o subconjunto
if subset_sum == target_sum:
return subset, expanded
return Nonebacktracking
Para implementar a estratégia de backtracking, podemos seguir os seguintes passos:
1 - Parametros: índice atual, subconjunto atual e soma atual
2 - No inicio da funcao verificamos se o subconjunto atual é uma solução. Se for ENCONTRAMOS A SOLUÇÃO e podemos finalizar a função.
3 - Se a soma atual for maior que o objetivo não será possivel encontrar uma solução, então retornamos None.
4 - Para cada elemento a partir do índice atual, atualizamos o subconjunto e a soma atual e voltamos para o primeiro passo.
Exemplo [5, 4, 9] = 4
Red: unexplored solutions
Green: correct node
Blue: explored nodes
python code:
def subset_sum_backtracking(array: List[int], target_sum: int) -> Tuple[List[int], int] | None:
expanded = 0 # Counter to keep track of expanded nodes
def backtrack(start, current_subset, current_sum):
# Verifica se achamos o resultado
if current_sum == target_sum:
return current_subset
# Verifica se a soma atual é maior que o objetivo ou se já percorremos todo o vetor
if current_sum > target_sum or start >= len(array):
return None
for i in range(start, len(array)):
# Counter de nos expandidos
nonlocal expanded
expanded += 1
# Atualiza o subconjunto e a soma atual
new_subset = current_subset + [array[i]]
new_sum = current_sum + array[i]
result = backtrack(i + 1, new_subset, new_sum)
# Se achou o resultado retorna
if result is not None:
return result
# Se não achou, retorna None
return None
result = backtrack(0, [], 0)
print(f'Backtrack Expanded {expanded} nodes')
return result, expandedTestes
Todos os testes foram realizados em um processador 10th Generation Intel Core i7-1065G7 e 16BG de RAM.
Entradas
random.sample é uma função que retorna uma lista de elementos únicos de um determinado intervalo.
range representa o intervalo.
o ultimo numero(10 para o primeiro teste) representa o valor objetivo para o problema.
o codigo para todos os testes pode ser encontrado em: testes.py
# Testes variados
test_data = [
([1, 2, 3, 4, 5], 10),
([3, 7, 2, 8, 4], 15),
(random.sample(range(1, 11), 10), 12),
(random.sample(range(1, 51), 50), 70),
(random.sample(range(1, 101), 100), 123),
(random.sample(range(1, 201), 200), 234),
(random.sample(range(1, 501), 500), 567),
(random.sample(range(1, 1001), 1000), 123),
(random.sample(range(1, 1001), 1000), 1234),
(random.sample(range(1, 10001), 10000), 12345),
]Teste 1
Nesse primeiro teste, executamos os algoritmos com entradas variadas para podermos identificar quais testes poderiam ser relevantes para identificarmos as diferenças, vantagens e desvantagens dos algoritmos de brute force e backtracking.
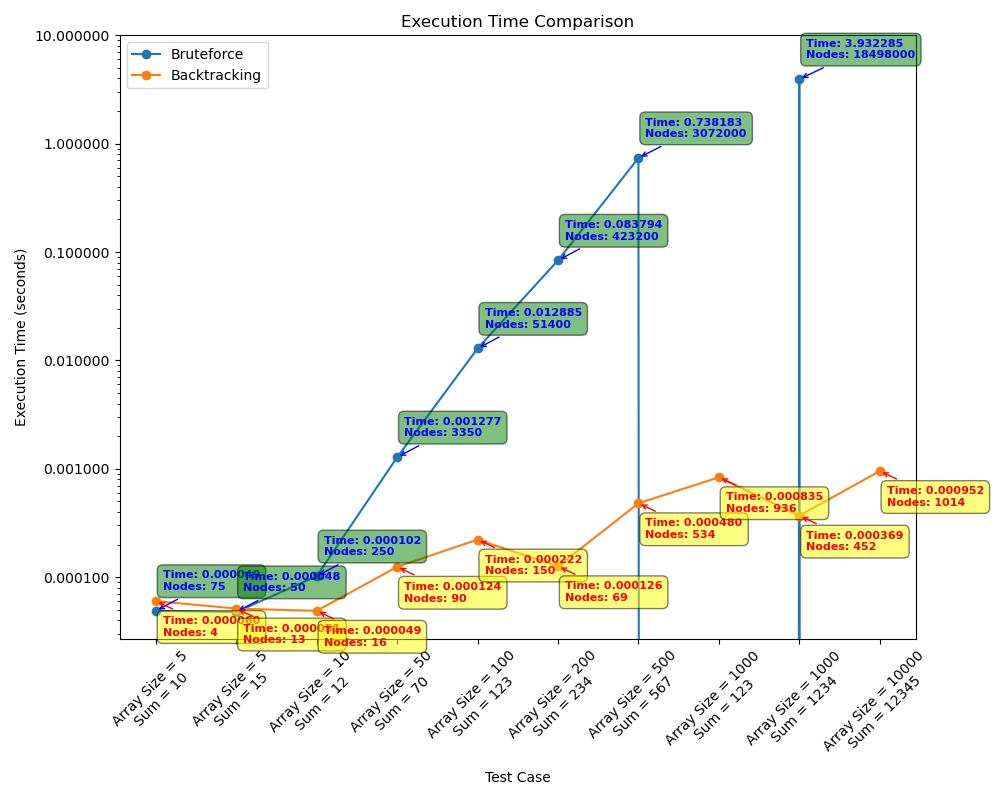
Teste 2
No teste 2 os algoritmos foram executados com entradas de tamanho crescente, sempre mantendo o valor da soma a metade do número de elementos do array. O objetivo desse teste é observar a variação de tempo conforme o tamanho do array vai aumentando com um valor de soma relativamente baixo.
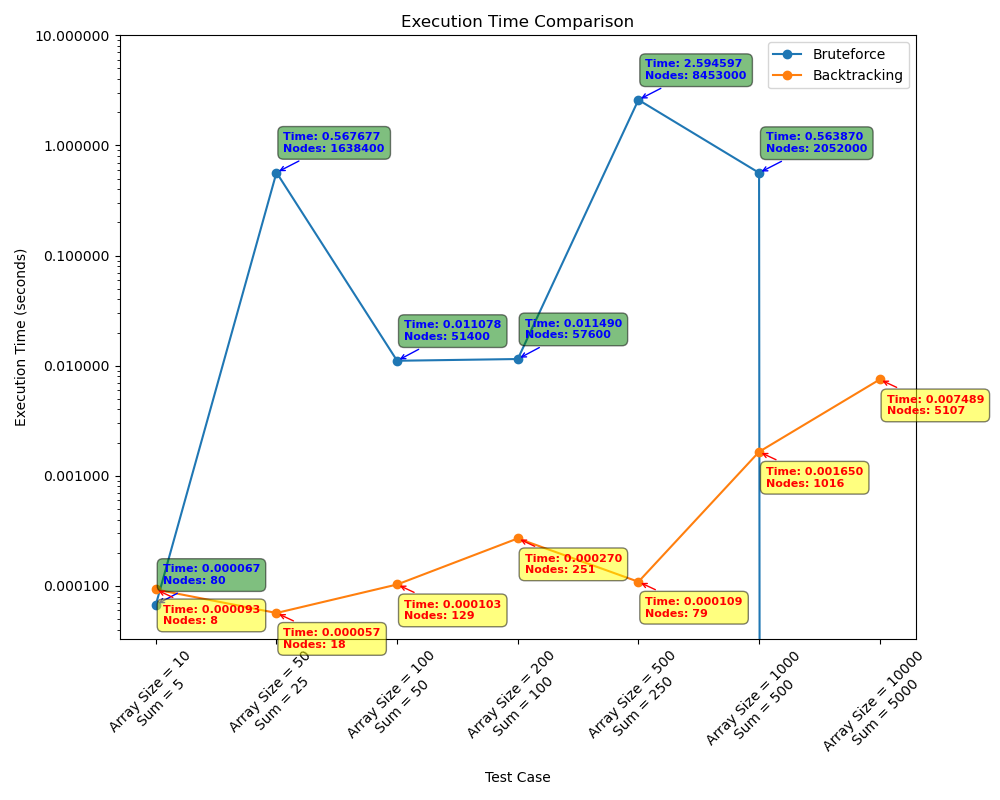
Teste 3
No teste 3 os algoritmos foram executados com entradas de tamanho crescente, sempre mantendo o valor da soma o dobro do número de elementos do array. O objetivo desse teste é observar a variação de tempo conforme o tamanho do array vai aumentando com um valor de soma relativamente alto.
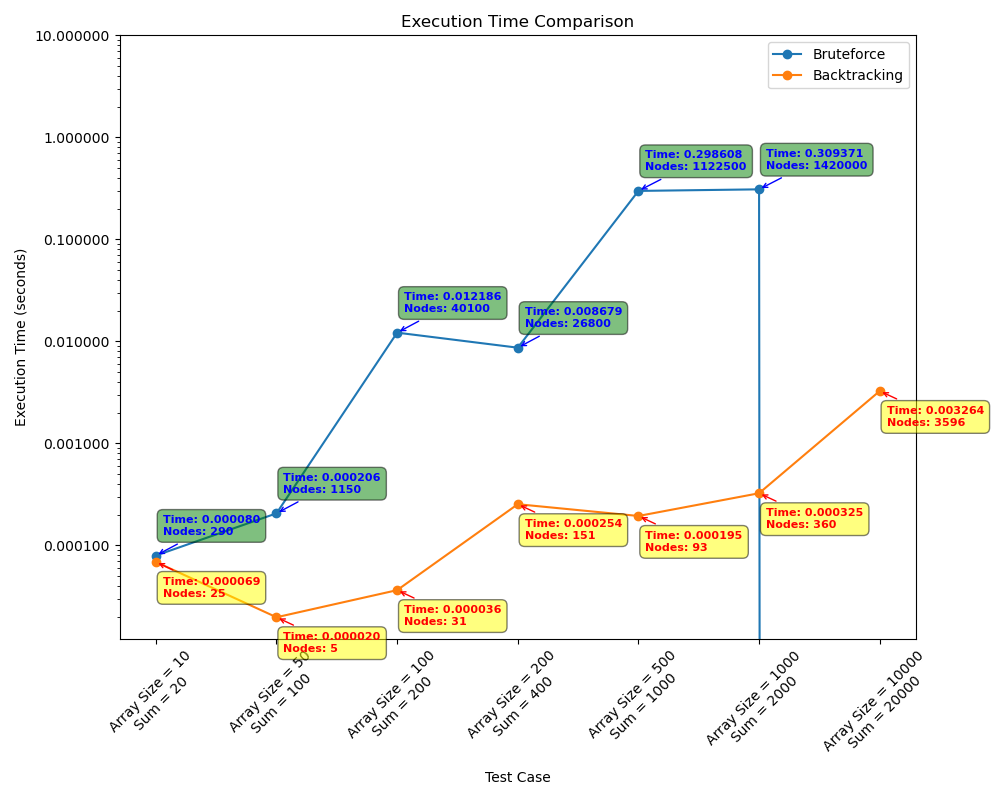
Teste 4
No teste 4 os algoritmos foram executados com o mesmo tamanho de array, com entradas de soma diferentes em ordem crescente. O objetivo é analisar a variação de tempo dos algoritmos conforme o valor da soma aumenta.
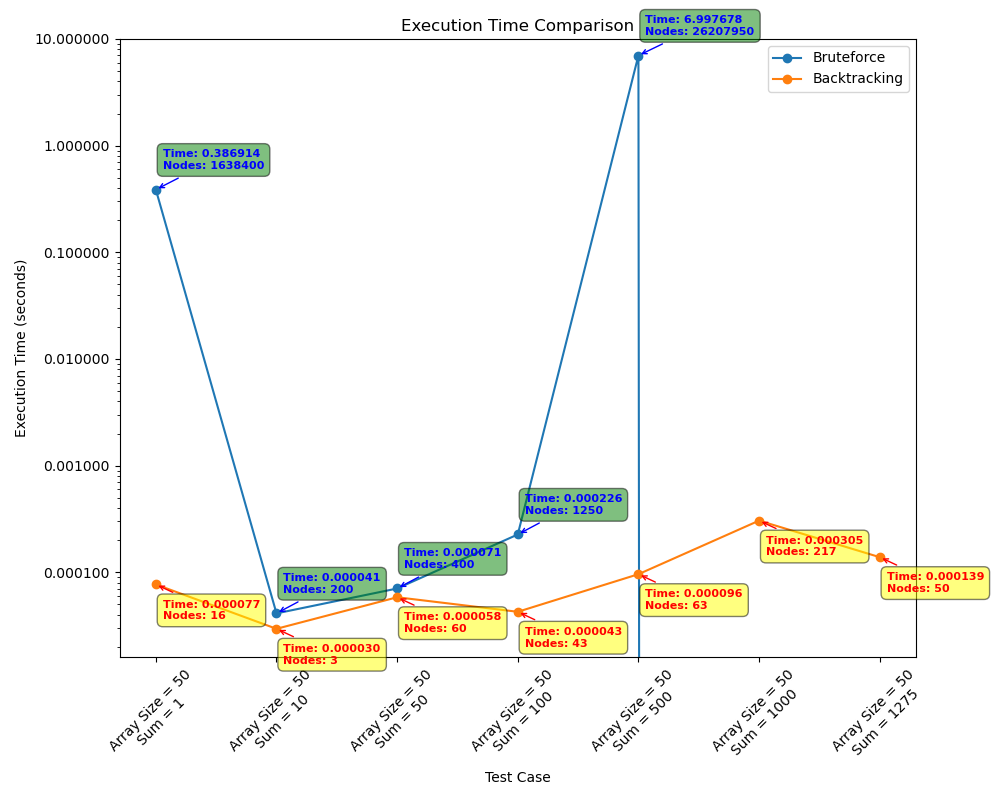
Teste 5
No teste 5 os algoritmos foram executados com o mesmo tamanho de array, com entradas de soma diferentes em ordem crescente. O objetivo é analisar a variação de tempo dos algoritmos conforme o valor da soma aumenta em um array relativamente médio (tamanho 2000).
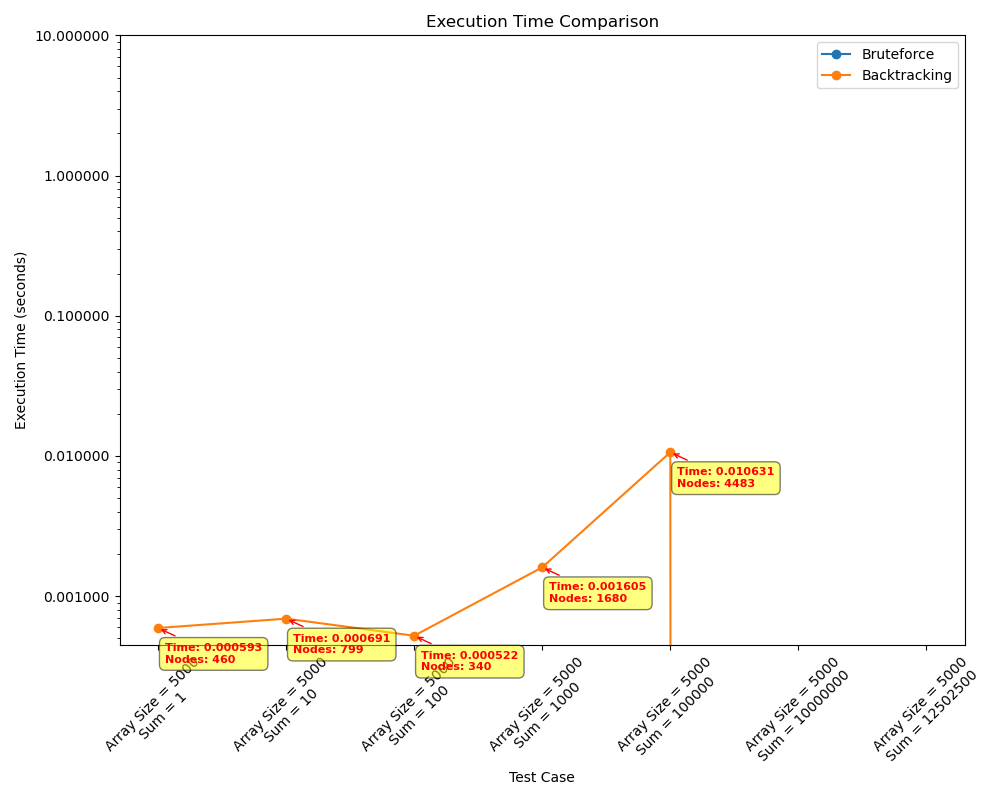
Comparações e Conclusões
A partir da análise dos dados obtidos com os testes realizados, podemos deduzir que o algoritmo de backtracking leva ligeira vantagem em relação ao algoritmo de força bruta em quase todas as situações.
Já no primeiro teste, o algoritmo de força bruta tem um execution time menor apenas nos dois primeiros casos, quando o tamanho do array era 5, assim que esse tamanho foi aumentado, o algoritmo de backtracking se mostrou bem mais eficiente.Vale lembrar que em 2 das entradas o algoritmo de backtracking deu timeout.
No segundo teste apenas no primeiro valor de entrada o algoritmo de força bruta obteve vantagem, decretando que quanto mais o tamanho do array aumenta maior a diferença de execution time do algoritmo de força bruta para o de backtracking, também é importante destacar que a quantidade de nodos visitados aumenta conforme o tamanho do array aumenta, o que impacta diretamente no tempo de execução do algoritmo.
O segundo teste foi executado com uma soma sendo metade do maior valor possivel do array, já no terceiro essa soma foi o dobro do maior valor possível do array, os resultados foram parecidos. Em resumo o Backtracking obteve vantagem no quesito tempo de execução em todas as entradas. Uma diferença perceptível notada entre o teste 2 e o 3, foi a constância dos resultados, isso provavelmente se deve que com uma soma de maior valor existe maiores possibilidades de ser encontrado um subconjunto e por isso o fator randômico é minimizado.
No quarto teste podemos observar como os algoritmos lidam com a mudança do valor da soma, podendo ser observado certa constância no algortimo de backtracking, enquanto que o algoritmo de força bruta possui melhores tempos quando o valor da soma é igual, ou o dobro do tamanho do array. Isso pode ser explicado pela quantidade de combinações possíveis que podem ser encontradas, que em valores muito baixos e muito altos são poucas e dificulta para um algoritmo que analisa nodo por nodo.
No quinto teste, foi testado a mesma situação do quarto teste, porém com um tamanho de array bem maior, pode ser observado que o único valor em que o algoritmo de força bruta não deu timeout foi quando o valor da soma era igual ao valor do array, confirmando a tese proposta no parágrafo acima que o algoritmo de força bruta apresenta melhores resultados de tempo de execução quando submetidos a casos onde existem maiores quantidade de subconjuntos resultados na amostra. É importante observar que o algoritmo de backtracking se mantém estável, com um leve aumento no tempo de execução conforme o valor da soma aumenta.
O sexto teste segue a mesma linha dos testes 4 e 5, com a diferença do aumento do tamanho do array para 5000, isso permite observar o ponto onde o backtracking encontra o timeout, onde a soma era igual a 100000. O algoritmo de força bruta não foi capaz de executar nenhuma entrada desse teste.
Relatorio Final
O algoritmo de backtracking é mais eficiente que o algoritmo de brute force, pois ele não precisa gerar todas as combinações possíveis, ele vai gerando as combinações e verificando se a soma é igual ao objetivo, se não for ele volta e tenta outra combinação, descartando combinações impossiveis.
O algoritmo de brute force é mais simples de implementar, porém ele é muito ineficiente, pois ele gera todas as combinações possíveis e verifica se a soma é igual ao objetivo, então encontrar o objetivo de forma rapida se torna meio aleatório, pois depende da ordem que as combinações são geradas e calculadas.